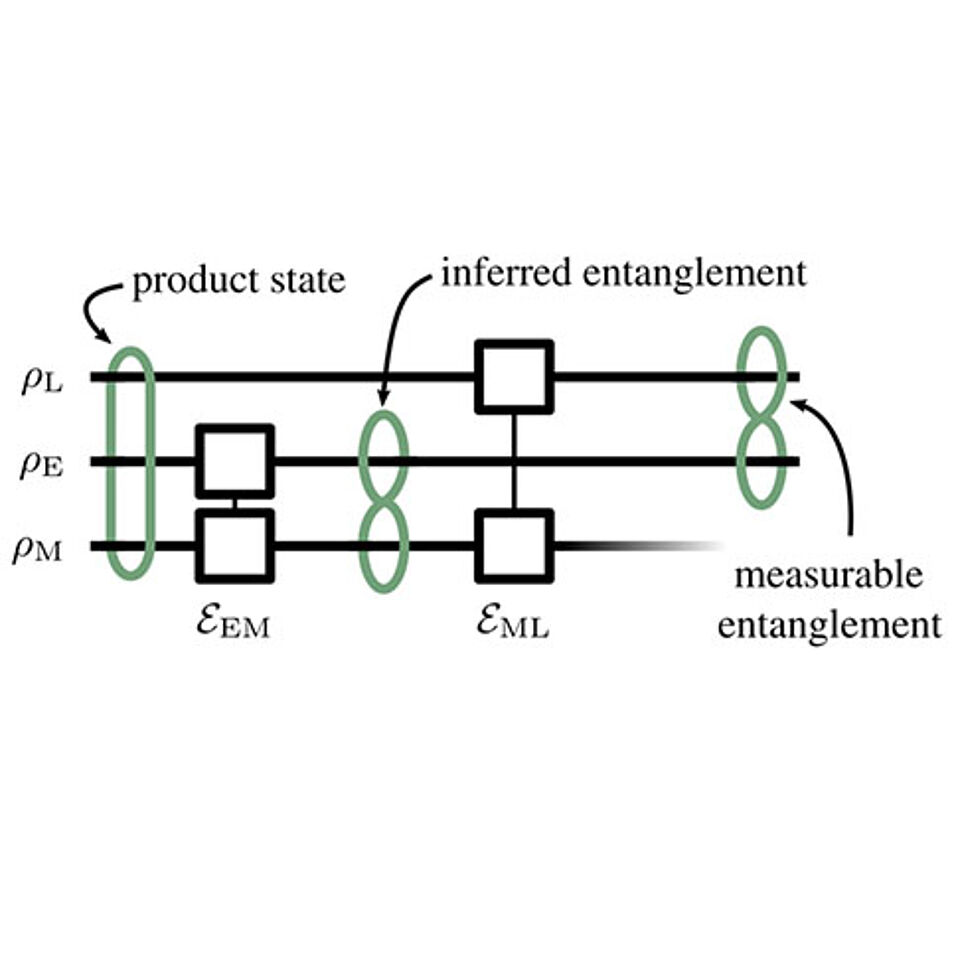
The theoretical prediction of the existence of optomechanical entanglement at all times in a system in its steady state is more than 10 years old [Genes et al, PRA 78, 032316 (2008)]. Still, the experimental realisation remains challenging. This is because it is conceptually difficult to access the state of the mechanical oscillator experimentally. In our work we propose a practical solution to infer this “stationary” entanglement without knowledge of the actual state of the mechanical oscillator.
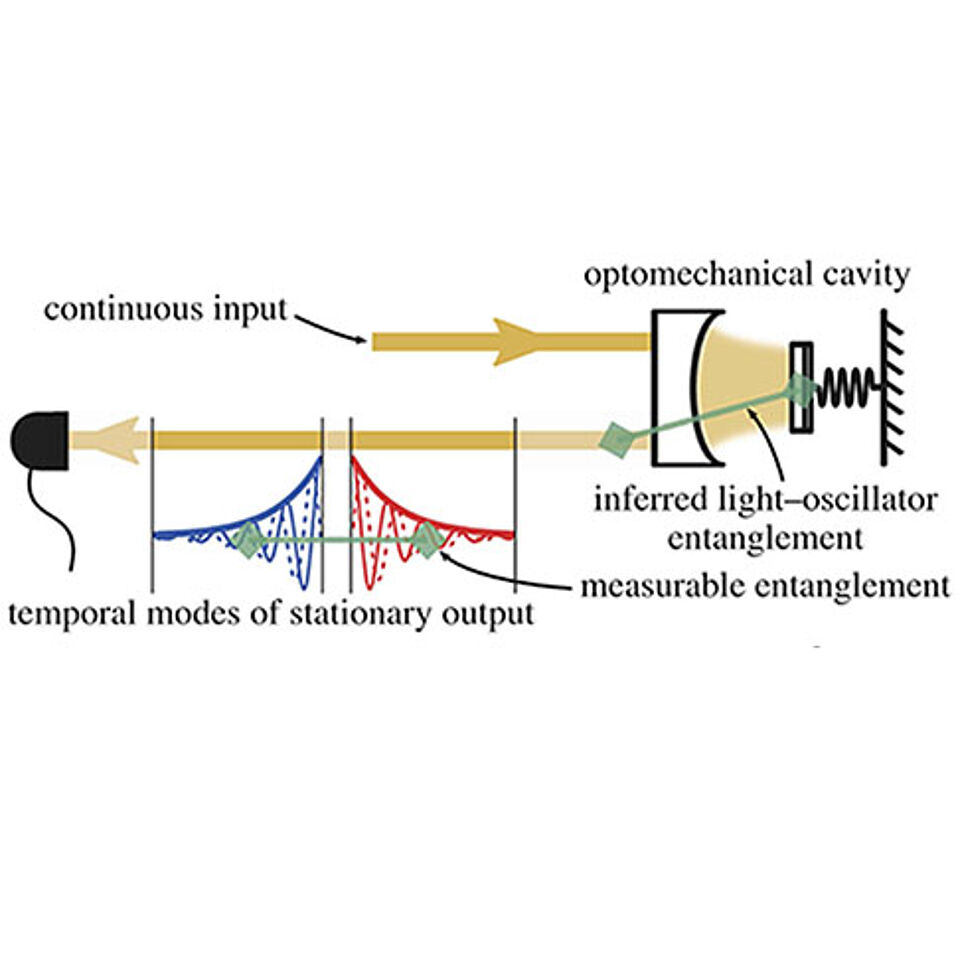
The scheme we propose consists of a non-sideband-resolved optomechanical system driven on resonance by a continuous-wave field; this is the typical configuration for continuous position- or force-sensors. The figure illustrates the logic: the continuously measured output field is decomposed — abstractly in postprocessing — into temporally ordered modes that can be measured. Our work shows that if the temporal modes are entangled, then the mechanical oscillator is entangled with the early temporal mode.
We show analytically that our scheme always detects stationary optomechanical entanglement in the form of (squeezed) Einstein-Podolski-Rosen (EPR) quadratures of the output light. An experimental realisation is prone to noises and uncertainties that we did not model, therefore one should aim at strong violation of the EPR separability witness. We derive a formula for the violation, which is simple and tells how to best choose the parameters.
Publication:
Stationary optomechanical entanglement between a mechanical oscillator and its measurement apparatus
C. Gut, K. Winkler, J. Hoelscher-Obermaier, S. G. Hofer, R. Moghadas Nia, N. Walk, A. Steffens, J. Eisert, W. Wieczorek, J. A. Slater, M. Aspelmeyer, K. Hammerer
Phys. Rev. Research 2, 033244 (2020